परमाणु की संरचना के अध्ययन के लिए विभिन्न प्रतिरूप या मॉडल दिए गये है जो निम्न प्रकार है-
डाल्टन का परमाणु सिद्धांत (Dalton’s Model)
- प्रत्येक पदार्थ छोटे-छोटे कणों से मिलकर बना होता है, जिन्हें परमाणु (Atom) कहते हैं।
- परमाणु अविभाज्य है, अर्थात इसे न तो नष्ट किया जा सकता है और न ही उत्पन्न किया जा सकता है।
- एक ही तत्व के सभी परमाणु भौतिक और रासायनिक गुणों में समान होते हैं, जबकि भिन्न-भिन्न तत्वों के परमाणु के गुण भिन्न-भिन्न होते हैं।
- विभिन्न तत्वों के परमाणु हाइड्रोजन (Hydrogen) के परमाणु से निर्मित होते हैं। सबसे भारी परमाणु की त्रिज्या हाइड्रोजन की लगभग 10 गुना और द्रव्यमान लगभग 250 गुना होता है।
- परमाणु स्थायी और विद्युत उदासीन (Electrically Neutral) होता है।
थॉमसन का परमाणु प्रतिरूप (Thomson’s Model)
- परमाणु विद्युत उदासीन (Electrically Neutral) होता है क्योंकि परमाणु का धन आवेश (Positive Charge) और ऋण आवेश (Negative Charge) बराबर होता है।
- परमाणु एक धन आवेशित गोला होता है, जिसकी त्रिज्या 10-10 मीटर होती है, और इसमें इलेक्ट्रॉन्स (Electrons) इस प्रकार स्थित होते हैं जैसे तरबूज में बीज या लड्डू में इलायची के दाने।
- परमाणु का धन आवेश और द्रव्यमान (Mass) पूरे गोले में समान रूप से वितरित होता है।
थॉमसन प्रतिरूप के दोष (Drawbacks of Thomson’s Model)
- इस प्रतिरूप की सहायता से परमाणुओं के स्पेक्ट्रम (Spectrum) की व्याख्या नहीं की जा सकती।
- इस प्रतिरूप से α-कणों (Alpha Particles) के प्रकीर्णन (Scattering) को समझाया नहीं जा सकता।
रदरफोर्ड का परमाणु प्रतिरूप (Rutherford’s Model)
रदरफोर्ड द्वारा स्वर्ण की पतली पन्नी पर α-कणों के प्रकीर्णन का प्रयोग:
रदरफोर्ड ने परमाणु की संरचना का अध्ययन करने के लिए α-कणों (Alpha Particles) का उपयोग किया।
प्रायोगिक व्यवस्था:
- रेडियोधर्मी (Radioactive) पदार्थ, जैसे पोलोनियम (Polonium) से α-कण उत्सर्जित होते हैं।
- ये कण सीसे के पर्दे में बने छिद्र से होकर स्वर्ण पन्नी (Gold Foil) पर आपतित होते हैं।
- स्वर्ण पन्नी के बाहर एक जिंक सल्फाइड (Zinc Sulfide) का पर्दा होता है जो प्रकीर्णित कणों को ग्रहण करता है।
- जब α-कण इस पर्दे पर आपतित होते हैं, तो पर्दे पर चमक उत्पन्न होती है, जिसे सूक्ष्मदर्शी (Microscope) से देखा जाता है।
परिणाम:
- अधिकांश α-कण स्वर्ण पन्नी से बिना विचलित हुए निकल गए, जिससे यह निष्कर्ष निकला कि परमाणु लगभग खोखला (Hollow) होता है।
- कुछ α-कण बड़े कोण से विचलित हुए, जबकि कुछ स्रोत की ओर वापस लौट आए।
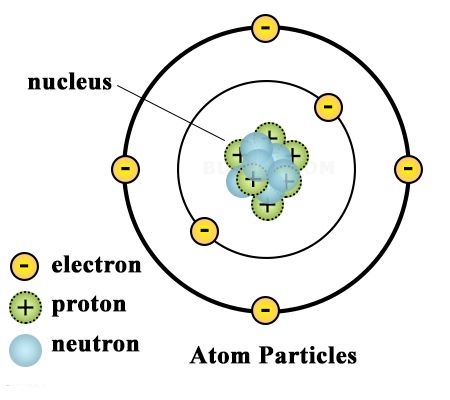
- परमाणु का संपूर्ण आवेश और द्रव्यमान (Mass) उसके केंद्र में एक सूक्ष्म बिंदु पर केंद्रित होता है, जिसे नाभिक (Nucleus) कहते हैं।
- इलेक्ट्रॉन्स (Electrons) नाभिक के चारों ओर वृत्ताकार कक्षाओं (Circular Orbits) में घूमते हैं।
रदरफोर्ड का निष्कर्ष:
- परमाणु के धन आवेश (Positive Charge) और द्रव्यमान (Mass) का अधिकांश भाग नाभिक में संचित होता है, जिसका व्यास 10-13 सेमी से भी कम होता है।
- नाभिक के चारों ओर इलेक्ट्रॉन्स का बादल (Cloud of Electrons) स्थित होता है।
- परमाणु विद्युत उदासीन (Electrically Neutral) होता है।
रदरफोर्ड के प्रकीर्णन सूत्र (Rutherford’s Scattering Formula):
[latex] \mathrm{N}_\theta=\frac{\mathrm{N}_0 \mathrm{nt}\left(2 Z e^2\right)^2}{16\left(4 \pi \varepsilon_0\right)^2 \mathrm{r}^2\left(\mathrm{mv}_0^2\right)^2} \times \frac{1}{\sin ^4 \frac{\theta}{2}} [/latex]
जहां:
[latex]N }[/latex]= प्रकीर्णित कणों की संख्या
[latex]n =[/latex] लक्ष्य में प्रति इकाई आयतन परमाणुओं की संख्या।
[latex]d = [/latex] लक्ष्य की मोटाई।
[latex]Z = }[/latex] लक्ष्य के नाभिक पर आवेश।
[latex]e = \alpha [/latex] -कण पर आवेश।
[latex]r =}[/latex] प्रकीर्णन की दूरी।
[latex]KE = \alpha [/latex] -कणों की गतिज ऊर्जा।
[latex]\epsilon_0 = [/latex] निर्वात का विद्युत स्थिरांक।
[latex]r_0=\frac{1}{4 \pi \varepsilon_0} \times \frac{(2 Z e)^2}{\left[\frac{1}{2} m_0^2\right.}=\frac{1}{4 \pi \epsilon_0} \frac{(2 Z e)^2}{E_K} [/latex]
जहाँ
EK = a-की गतिज ऊर्जा
बोर का परमाण्वीय प्रतिरूप (Bohr’s Atomic Model)
डेनमार्क के एक भौतिक विज्ञानी नील बोहर ने 1913 में परमाणु के स्थायित्व को समझाने के लिए क्वांटम की अवधारणा प्रस्तुत की। उन्होंने यह विचार दिया कि बड़ी वस्तुओं पर लागू होने वाले पुराने चिरसम्मत नियम, इलेक्ट्रॉन और प्रोटॉन जैसे उप-परमाण्वीय कणों पर सीधे लागू नहीं किए जा सकते।
बोहर ने अपनी अवधारणा के आधार पर निम्न परिकल्पनाएँ दीं:
- नाभिक (nucleus) के चारों ओर चक्कर लगाते हुए इलेक्ट्रॉन (electron) को वृत्तीय कक्षा (circular orbit) में घूमने के लिए आवश्यक अभिकेन्द्रीय बल (centripetal force), नाभिक और इलेक्ट्रॉन के मध्य स्थिर वैद्युत आकर्षण (electrostatic attraction) द्वारा प्रदान किया जाता है:
\[
\varepsilon_0: मूल आकाश की विद्युतगुणीयता 8.85 \times 10^{-12} \, \mathrm{C^2 \, N^{-1} \, m^{-2}}
\]
m: इलेक्ट्रॉन का द्रव्यमान
v: इलेक्ट्रॉन की कक्षीय वेग
r: इलेक्ट्रॉन की कक्षीय त्रिज्या
Z: हाइड्रोजन परमाणु का परमाणु क्रमांक (हाइड्रोजन के लिए } Z = 1
हाइड्रोजन परमाणु में बल संतुलन का सूत्र:
\[
\frac{1}{4 \pi \varepsilon_0} \cdot \frac{Z e^2}{r^2} = \frac{m v^2}{r}
\]
यह सूत्र कोलंब बल और अभिकेंद्रीय बल के संतुलन को दर्शाता है।
- इलेक्ट्रॉन केवल उन कक्षाओं में घूम सकते हैं जिनमें उनका कोणीय संवेग (angular momentum) क्वांटम का पूर्ण गुणज हो:
m v r = \frac{n h}{2 \pi} \quad \ldots \quad \text{(ii)}
जहाँ:
- n = मुख्य क्वांटम संख्या (principal quantum number)
- \hbar = h / (2π), प्लांक का स्थिरांक (Planck’s constant)
- परमाणु में इलेक्ट्रॉन केवल विशिष्ट ऊर्जा स्तरों (discrete energy levels) पर स्थित होते हैं और इन कक्षाओं में घूमने पर ऊर्जा का विकिरण नहीं करते।
- बाह्य कक्षा (outer orbit) की ऊर्जा, आंतरिक कक्षा (inner orbit) की ऊर्जा से अधिक होती है। जब इलेक्ट्रॉन बाह्य कक्षा से आंतरिक कक्षा में जाता है, तो यह ऊर्जा विकिरित (emit) करता है, जबकि आंतरिक कक्षा से बाह्य कक्षा में जाने पर ऊर्जा का अवशोषण (absorb) करता है:
[latex] \Delta E = E_{outer} – E_{inner} = h * f [/latex]
जहाँ:
- E_{outer} = बाहरी ऊर्जा स्तर (outer energy level)
- E_{inner} = आंतरिक ऊर्जा स्तर (inner energy level)
- f = विकिरण की आवृत्ति (frequency of radiation)
- उत्सर्जित या अवशोषित ऊर्जा सदैव विद्युत-चुंबकीय विकिरण (electromagnetic radiation) के रूप में होती है।
बोहर के सिद्धांत का गणितीय विश्लेषण (Mathematical Analysis of Bohr’s Model)
1. बल संतुलन और कोणीय संवेग
समीकरण (i) और (ii) से:
[latex]
\frac{1}{4 \pi \varepsilon_0} \cdot \frac{(Z e)e}{r^2} = \frac{m v^2}{r} \quad \ldots \text{(i)}
[/latex]
और
[latex]
m v r = \frac{n h}{2 \pi} \quad \ldots \text{(ii)}
[/latex]
2. n कक्षा में इलेक्ट्रॉन का वेग (Velocity of Electron in n Orbit):
समीकरण (ii) से \(m v r\) का मान समीकरण (i) में रखते हैं:
[latex]
\frac{1}{4 \pi \varepsilon_0} Z e^2 = \left(\frac{n h}{2 \pi r}\right) \cdot v
[/latex]
यहाँ से \(v\) (इलेक्ट्रॉन का वेग) के लिए पुनः व्यवस्थित करें:
[latex]
v = \frac{Z}{n} \cdot \frac{e^2}{2 \varepsilon_0 h} = \frac{Z}{n} v_0 \quad \ldots \text{(iii)}
[/latex]
जहाँ \(v_0\), हाइड्रोजन के पहले कक्षा (\(Z = 1\)) में इलेक्ट्रॉन का वेग है:
[latex]
v_0 = \frac{(1.6 \times 10^{-19})^2}{2 \times 8.85 \times 10^{-12} \times 6.625 \times 10^{-34}}
[/latex]
\(v_0\) की गणना करने पर:
[latex]
v_0 = 2.189 \times 10^6 \, \text{ms}^{-1} = \frac{c}{137} = 2.2 \times 10^6 \, \text{m/s}
[/latex]
जहाँ \(c = 3 \times 10^8 \, \text{m/s}\) निर्वात में प्रकाश की चाल है।
3. nवी कक्षा की त्रिज्या (Radius of n Orbit):
समीकरण (iii) से \(v\) का मान समीकरण (ii) में रखते हैं:
[latex]
m \left(\frac{Z}{n} \cdot \frac{e^2}{2 \varepsilon_0 h}\right) r = \frac{n h}{2 \pi}
[/latex]
यहाँ से \(r\) के लिए पुनः व्यवस्थित करें:
[latex]
r = \frac{n^2 Z e^2 h^2}{4 \pi^2 m e^4} = \frac{n^2}{Z} r_0 \quad \ldots \text{(iv)}
[/latex]
जहाँ \(r_0\), हाइड्रोजन के पहले कक्षा की त्रिज्या है:
[latex]
r_0 = \frac{8.85 \times 10^{-12} \times (6.625 \times 10^{-34})^2}{3.14 \times 9.11 \times 10^{-31} \times (1.6 \times 10^{-19})^2}
[/latex]
\(r_0\) की गणना करने पर:
[latex]
r_0 = 0.529 \times 10^{-10} \, \text{m} = 0.53 \, \text{Å}
[/latex]
3. n वी कक्षा में कुल ऊर्जा (Total Energy in n Orbit):
समीकरण (i) से गतिज ऊर्जा (KE):
[latex]
KE = \frac{1}{2} mv^2 = \frac{Z^2 e^4}{8 \varepsilon_0^2 h^2}
[/latex]
स्थितिज ऊर्जा (PE):
[latex]
PE = -\frac{1}{4 \pi \varepsilon_0} \cdot \frac{(Ze)(-e)}{r} = -2 KE \quad \text{(i.e., \(PE = -2 KE\))}
[/latex]
नवी कक्षा की कुल ऊर्जा:
[latex]
E = KE + PE = -2 KE + KE = -KE = -\frac{Z^2 e^4}{8 \varepsilon_0^2 h^2} \quad \ldots \text{(v)}
[/latex]
जहाँ:
[latex]
E_0 = -\frac{(9.11 \times 10^{-31}) \cdot (1.6 \times 10^{-19})^4}{8 \times (8.85 \times 10^{-12})^2 \cdot (6.625 \times 10^{-34})^2} = -13.6 \, \text{eV}
[/latex]
4. nवी कक्षा में इलेक्ट्रॉन का आवर्तकाल:
[latex]
T = \frac{2 \pi}{v} = \frac{2 \pi r}{v}
[/latex]
समीकरण (iii) से \(v\) का मान रखकर \(T\):
[latex]
T = \frac{n^3}{Z^2} \cdot \left(\frac{4 \pi^2 h^3 \varepsilon_0^2}{m e^4}\right) = \frac{n^3}{Z^2} T_0
[/latex]
जहाँ:
[latex]
T_0 = \frac{4 \times (8.85 \times 10^{-12})^2 \cdot (6.625 \times 10^{-34})^3}{(9.11 \times 10^{-31}) \cdot (1.6 \times 10^{-19})^4} = 1.51 \times 10^{-16} \, \text{सेकंड}
[/latex]
5. nवी कक्षा में घूर्णन आवृत्ति:
[latex]
\nu = \frac{1}{T} = \frac{Z^2}{n^3} \cdot \left(\frac{m e^4}{4 h^3 \varepsilon_0^2}\right) = \frac{Z^2}{n^3} \nu_0
[/latex]
जहाँ:
[latex]
\nu_0 = \frac{(9.11 \times 10^{-31}) \cdot (1.6 \times 10^{-19})^4}{4 \cdot (8.85 \times 10^{-12})^2 \cdot (6.625 \times 10^{-34})^3} = 6.6 \times 10^{15} \, \text{Hz}
[/latex]
6. फोटोन की तरंगदैर्ध्य (Wavelength of Photon):
A. कक्षाओं के बीच ऊर्जा अंतर:
[latex]
\Delta E = E_n – E_m = -\frac{13.6 Z^2}{n^2} – \left(-\frac{13.6 Z^2}{m^2}\right) = 13.6 Z^2 \left(\frac{1}{m^2} – \frac{1}{n^2}\right)
[/latex]
समीकरण:
[latex]
\Delta E = h \nu = \frac{h c}{\lambda}
[/latex]
B. रिडबर्ग का समीकरण:
[latex]
\frac{1}{\lambda} = R \cdot Z^2 \left(\frac{1}{m^2} – \frac{1}{n^2}\right)
[/latex]
जहाँ:
[latex]
R = R_0 \cdot Z^2 = \frac{m e^4}{8 \varepsilon_0^2 h^3 c} = \frac{(9.11 \times 10^{-31}) \cdot (1.6 \times 10^{-19})^4}{8 \cdot (8.85 \times 10^{-12})^2 \cdot (6.625 \times 10^{-34})^3 \cdot 3 \times 10^8}
[/latex]
[latex]
= 1.097 \times 10^7 \, \text{m}^{-1} = 1.097 \times 10^{-3} \, \text{Å}^{-1} \quad (\text{हाइड्रोजन के लिए})
[/latex]
यदि नाभिक स्थिर नहीं है (अर्थात् नाभिक का द्रव्यमान, परिक्रमण करने वाले कण जैसे इलेक्ट्रॉन से बहुत ज्यादा नहीं है), तो:
[latex]
R = \frac{R_0}{1 + \frac{m}{M}}
[/latex]
जहाँ:
[latex]
m = \text{परिक्रमण करने वाले कण का द्रव्यमान} \quad \text{तथा} \quad M = \text{नाभिक का द्रव्यमान}
[/latex]
