Dipole moment in hindi, Electric dipole in hindi, विद्युत द्विध्रुव एवं द्विध्रुव आघूर्ण
विद्युत द्विध्रुव (Electric dipole)
अल्प दूरी पर रखे हुए दो समान तथा विपरित आवेशों का निकाय विद्युत द्विध्रुव कहलाता है।
कुछ अणुओं में धन व ऋण आवेशों के केन्द्र एक जगह नहीं होते जिसके परिणामस्वरूप विद्युत द्विध्रुव बनते है। ऐसे परमाणु अध्रुवीय होते है, क्योंकि उनके धन तथा ऋण आवेशों के केन्द्र एक जगह मिलते है। विद्युत क्षेत्र को आरोपित कर उनको धु्रवित बनाया जाता है। अतः इन्हें प्रेरित द्विध्रुव कहते है।
द्विध्रुव आघूर्ण (Dipole moment)
किसी आवेश के परिमाण तथा आवेशों के मध्य दूरी का गुणनफल द्विध्रुव आघूर्ण कहलाता है। यह प्रत्येक द्विध्रुव का अभिलाक्षणिक गुण है।
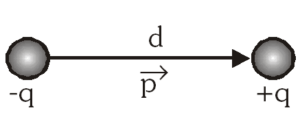
[katex display=true] \vec{P}=q \vec{d} [/katex]
द्विध्रुव आघूर्ण के गुण (Properties of dipole moment)
- यह एक सदिश राशि, जिसकी दिशा ऋण आवेश से धन आवेश की ओर होती है।
- इसका मात्रक कूॅलाम × मीटर (या सेमी) होता है। तथा प्रायोगिक मात्रक डिबाॅई (debye) होता है।
- द्विध्रुव आघूर्ण का विमीय सूत्र [LTA] होता है।
- दो परमाणुओं की विद्युत ऋणात्मकता में अंतर बढ़ने पर द्विध्रुव आघूर्ण का मान भी बढ़ता है। अतः HF > HCl > HBr > HI
- दो समान परमाणुओं से मिलकर बने अणु का द्विध्रुव शून्य होता है। H2, Cl2, F2 Br2 O2 , N2 आदि
- बहुपरमाण्वीय अणु का द्विध्रुव आघूर्ण उस बहुपरमाण्वीय अणु में उपस्थित सभी ध्रुवीय बन्धो के द्विध्रुव आघूर्ण के सदिश योग के बराबर होता है।
डिबाॅई (debye) की परिभाषा
दो बिन्दु समान व विपरीत आवेश जिनका मान 10–10 फ्रेंकलिन हो और उनके मध्य की दूरी 1 Å हो तो उनके द्विध्रुव आघूर्ण का मान 1 डिबाॅई होता है।
1 D = 10−18 e.s.u X c. m (e.s.u = स्थिर विद्युत मात्रक)
ध्रुवीय अणु और अध्रुवीय अणु (Polar and non-polar molecules)
कोणीय संरचना वाले अणुओं का द्विध्रुव आघूर्ण निश्चित होता है तथा ऐसे अणु ध्रुवीय अणु कहलाते है। जैसे H2O
रेखीय, समतल, त्रिकोणीय तथा चतुष्फलकीय संरचना वाले अणुओं में यदि केन्द्रीय परमाणु से जुड़े सभी परमाणु समान होते है तो उन अणुओं का द्विध्रुव आघूर्ण शून्य होता है ये अणु अध्रुवीय अणु कहलाते है। जैसे CO2 , BeCl2
द्विध्रुव के कारण विद्युत क्षेत्र (Electric field due to dipole)
द्वि ध्रुव के दोनों आवेशों के कारण विद्युत क्षेत्र रहता है। द्विध्रुव के कारण उत्पन्न विद्युत क्षेत्र की तीव्रता (Intensity of electric field ) ज्ञात करने के लिए उस बिंदु पर स्थित इकाई धन आवेश पर द्विध्रुव के प्रत्येक आवेश के कारण लगने वाले बल को ज्ञात किया जाता है। और अध्यारोपण सिद्धांत का उपयोग करके सदिश योग द्वारा परिणामी बल प्राप्त करते हैं।
द्विध्रुव की अक्ष रेखा पर विद्युत क्षेत्र की तीव्रता (Electric field on the axial line of a dipole)
द्वि ध्रुव के धन और ऋण आवेशों में से गुजरने वाली रेखा को द्विध्रुव की अक्ष रेखा कहा जाता है।
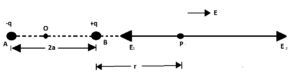
माना कि एक द्विध्रुव दो बिंदु आवेशों +q तथा -q जो कि एक दूसरे से अल्प दूरी 2a पर स्थित है। चित्रानुसार बिंदु p जो की द्विध्रुव की अक्ष रेखा पर तथा द्विध्रुव के केंद्र से r दूरी पर स्थित है।
यदि बिंदु पर आवेश के कारण विद्युत क्षेत्र होतो
[katex display=true] \left|E_{1}\right|=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{A P^{2}}=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{(r+a)^{2}} [/katex] ……….. (1)
इसकी दिशा PA की तरफ होगी
इसी तरह से बिंदु आवेश के कारण विद्युत क्षेत्र की दो हो तो
[katex display=true] .\left|E_{2}\right|=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{B P^{2}}=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{(r-a)^{2}} [/katex] ………….(2)
इसकी दिशा BP की तरफ होगी
क्योंकि E1 और E2 संरेख सदिश में है, जो कि विपरीत दिशा पर स्थित है। तथा |E2| > |E1|
अतः परिणामी तीव्रता E का P बिंदु पर मान होगा
|E2| = |E2| – |E1| ………………… (3)
समीकरण 1 तथा 2 से मान समीकरण 3 में रखने पर
[katex display=true] |E|=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{(r-a)^{2}}-\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{(r+a)^{2}} [/katex]
[katex display=true] =\frac{q}{4 \pi \varepsilon_{0}}\left[\frac{1}{(r-a)^{2}}-\frac{1}{(r+a)^{2}}\right. [/katex]
[katex display=true]=\frac{q}{4 \pi \varepsilon_{0}}\left[\frac{(r+a)^{2}-(r-a)^{2}}{\left(r^{2}-a^{2}\right)^{2}}\right. [/katex]
[katex display=true] =\frac{q}{4 \pi \varepsilon_{0}} \cdot \frac{4 a r}{\left(r^{2}-a^{2}\right)^{2}} [/katex]
[katex display=true] =\frac{q}{4 \pi \varepsilon_{0}} \cdot \frac{2 a \times 2 r}{\left(r^{2}-a^{2}\right)^{2}} [/katex]
चूँकि q x 2a = |p| = द्विध्रुव आघूर्ण
अतः
[katex display=true] |E|=\frac{|p|}{4 \pi \varepsilon_{0}} \cdot \frac{2 r}{\left(r^{2}-a^{2}\right)^{2}} [/katex]
यदि द्विधुव्र के लिए 2a << r तो
[katex display=true] |E|=\frac{|p|}{4 \pi \varepsilon_{0}} \cdot \frac{2 r}{r^{4}}=\frac{2|p|}{4 \pi \varepsilon_{0} r^{3}} [/katex]
अतः
[katex display=true] |E| \propto \frac{1}{r^{3}} [/katex]
यह दिशा BP की ओर होगा
Dipole moment in hindi, Electric dipole in hindi,
द्विध्रुव की निरक्ष रेखा पर विद्युत क्षेत्र की तीव्रता (Electric field intensity equatorial line of dipole)
द्विध्रुव के धन और ऋण आवेशों में से गुजरने वाली अक्ष रेखा के लम्बवत मध्य बिंदु से होकर गुजरने वाली रेखा को द्विध्रुव की निरक्ष रेखा (equatorial line) कहा जाता है।
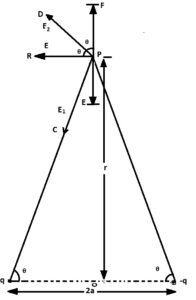
माना कि एक द्विध्रुव दो बिंदु आवेशों +q तथा -q जो कि एक दूसरे से अल्प दूरी 2a पर स्थित है। चित्रानुसार बिंदु p जो की द्विध्रुव की निरक्ष रेखा पर तथा द्विध्रुव के केंद्र से r दूरी पर स्थित है।
[katex display=true]\left|E_{1}\right|=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{A P^{2}}[/katex]
हम जानते है कि
(AP)2 = (OP)2 + (OA)2
= r2 + a2
अतः
[katex display=true]\left|E_{1}\right|=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{\left(r^{2}+a^{2}\right)}[/katex] …………. (1)
चित्रानुसार रेखा PR रेखा BA के समांतर है और E1 को PC द्वारा दिखाया गया है।
माना कि ∠PBA = θ = ∠RPC
हम E1 को लम्बवत सदिशों, E1cosθ जो कि PR की ओर है तथा E1sinθ जो कि PO की तरफ है मान (वियोजित) सकते है।
इसी तरह से B बिंदु पर स्थित आवेश +q के कारण P बिन्दु पर यदि विद्युत आवेश की तीव्रता E2 हो तो
[katex display=true] \left|E_{2}\right|=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{B P^{2}}=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{\left(r^{2}+a^{2}\right)} [/katex] ………….. (2)
चित्र में E2 को PD द्वारा दर्शाया गया है।
हम E2 को दो लम्बवत सदिशों E2cosθ जो की PR की तरफ है तथा E2sinθ जो की PF की तरफ है में वियोजित कर सकते है
|E1| = |E2|
अतः PO की दिशा E1sinθ तथा PF दिशा में घटक E2sinθ बराबर तथा एक दुसरे के विपरीत दिशा में होने के कारण एक दुसरे को नष्ट कर देंगे
परंतु PR दिशा में घटक एक ही दिशा में होने के कारण जुड़ जाएंगे तथा P बिंदु पर परिणामी विद्युत क्षेत्र की तीव्रता (E) PR दिशा में होगी तथा इसका मान निम्न प्रकार होगा
|E| = E1cosθ + E2cosθ
= 2E1cosθ
अतः
[katex display=true] |E|=\frac{2}{4 \pi \varepsilon_{0}} \cdot \frac{q}{\left(r^{2}+a^{2}\right)} \cdot \cos \theta [/katex]
[katex display=true] =\frac{2}{4 \pi \varepsilon_{0}} \cdot \frac{q}{\left(r^{2}+a^{2}\right)} \cdot\left(\frac{O B}{B P}\right) [/katex]
[katex display=true] =\frac{2}{4 \pi \varepsilon_{0}} \cdot \frac{q}{\left(r^{2}+a^{2}\right)} \cdot \frac{a}{\sqrt{r^{2}+a^{2}}} [/katex]
[katex display=true]=\frac{q \times 2 a}{4 \pi \varepsilon_{0}\left(r^{2}+a^{2}\right)^{3 / 2}}[/katex]
द्विध्रुव आघूर्ण |p| = q X 2a
अतः
[katex display=true]|E|=\frac{p}{4 \pi \varepsilon_{0}\left(r^{2}+a^{2}\right)^{3 / 2}}[/katex]
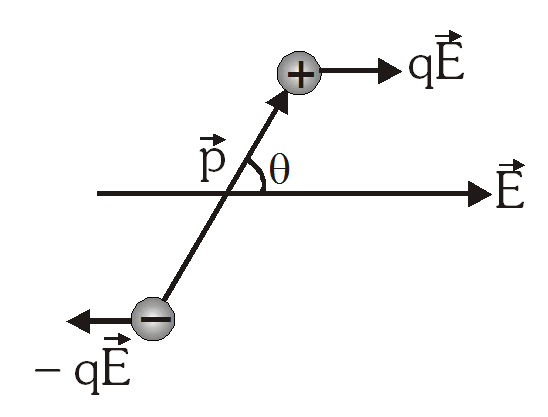
समरूप विद्युत क्षेत्र में रखे हुए द्विध्रुव के लिये द्विध्रुव आघूर्ण (Dipole moment for dipole Placed in uniform Electric Field)
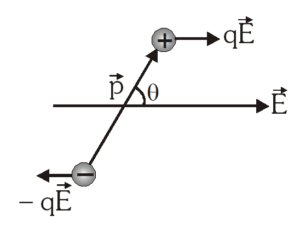
चित्रानुसार P द्विध्रुव आघूर्ण का एक द्विध्रुव, विद्युत क्षेत्र की दिशा के साथ θ कोण पर रखा हुआ है।
द्विध्रुव के आवेश बल qE अनुभव
[katex display=true] \overrightarrow{F_{n e t}}=[q \vec{E}+(-q) \vec{E}]=0 [/katex]
अतः हम कह सकते हैं कि जब एक द्विध्रुव समरूप विद्युत क्षेत्र में होता है तो द्विध्रुव पर परिणामी बल शून्य होता है। परन्तु उनकी क्रिया रेखा के मध्य दूरी के साथ समान तथा विपरीत बल कार्यरत होते हैं, जो बल युग्म उत्पन्न करते हैं जो द्विध्रुव को विद्युत क्षेत्र की दिशा में संरेखीय करने का प्रयास करते हैं।
इस बलयुग्म के कारण बलाघूर्ण t (tau)
= बल × बलों की क्रिया रेखा के मध्य दूरी
= qE X d Sinθ = pE Sinθ
Dipole moment in hindi, Electric dipole in hindi,
इन्हें भी पढ़े
- What is NEET? How to prepare for NEET Exam
- NEET क्या है? NEET परीक्षा की तैयारी कैसे करें
- How to Prepare For JEE Main & Advanced Exam
बाहरी कड़ियाँ
- Learn how to make a website – aliseotools.com
- How to Stop Hair Fall Naturally in Hindi
Dipole moment in Hindi, Electric dipole in Hindi,







