Home » आवेश संरक्षण तथा आवेश का क्वांटीकृत सिद्धांत, कुलाम का नियम

आवेश संरक्षण तथा आवेश का क्वांटीकृत सिद्धांत, कुलाम का नियम

Hamid ali April 7, 2021 भौतिक विज्ञान (Physical Sciences)

SaveSavedRemoved 4

Deal Score+2

0 3088

Deal Score+2

आवेश संरक्षण का सिद्धांत तथा आवेश का क्वांटीकृत सिद्धांत (Theory of Conservation of Charge and Quantization of Charge )

आवेश संरक्षण का सिद्धांत (Theory of Conservation of Charge)

इस नियम के अनुसार आवेश एक संरक्षित राशि (conserved unit) है। इसे न तो उत्पन्न किया जा सकता है, और ना ही नष्ट किया जा सकता है। इसे एक वस्तु से दूसरी वस्तु में स्थानांतरित किया जा सकता है। यह बेंजामिन फ्रैंकलिन द्वारा दिया गया।

आवेश सरंक्षण का सबसे अच्छा उदाहरण रेडियो एक्टिव क्षय है।

₉₂U²³⁸        →     ₉₀Th²³⁴ + ₂He⁴

  92                   90    +   2 

पहले आवेश q = 92

बाद में आवेश q = 90+2 =  92

किसी निकाय में भिन्न-भिन्न प्रकृति का आवेश (Charge) स्थित हो तो। उस निकाय का कुल आवेश सभी आवेशों के बीज गणितीय योग के बराबर होता है। इस गुण को आवेशों की योजकता (Additivity of Electric Charges ) कहते हैं।

∑q = (+q₁) + (-q₂) + (q₃)

Question.1

किसी निकाय में +q, -2q, +3q तथा +5q आवेश हो तो निकाय का कुल आवेश कितना होगा ?

Solution

q = (+q) +  (-2q) + (+3q) + (+5q)

          =9q-2q

          = 7q ans

युग्म उत्पादन (Pair Production)

यह एक प्रक्रिया है जिसके परिणामस्वरूप फोटॉन को इलेक्ट्रॉन-पॉज़िट्रॉन जोड़ी में परिवर्तित किया जाता है। नाभिकीय अभिक्रियाओं में जब अधिक ऊर्जा के फोटॉन (1.02MeV से अधिक) की द्रव्य के अन्योन्य क्रिया करते है तो एक इलेक्ट्रॉन तथा एक पॉज़िट्रॉन उत्पन्न होता है।

यहाँ 1.MeV का अर्थ मेगा इलेक्ट्रॉन वाल्ट है।

(adsbygoogle = window.adsbygoogle || []).push({});

आवेश का क्वांटीकृत / क्वांटीकरण  सिद्धांत (Theory of Quantization of Charge)

आवेश एक क्वांटीकृत राशि है यह हमेशा इलेक्ट्रॉन के पूर्ण गुणज के रूप में पाया जाता है। अर्थात

q = ne

n = इलेक्ट्रॉनों की संख्या = 1, 2, 3, 4,……n

e= इलेक्ट्रॉन पर आवेश = 1.6 x 10^-19C

आवेश की परमाणुकता (Atomicity of Charge)

इसके अनुसार आवेश को विभाजित नहीं किया जा सकता है।

Question.2

किसी धातु की सतह से 100 इलेक्ट्रॉन निकाले गए तो आवेश का मान ज्ञात कीजिए तथा इसकी प्रकृति कैसी होगी?

Solution

n = इलेक्ट्रॉनों की संख्या = 100

 e= इलेक्ट्रॉन पर आवेश = 1.6 x 10^-19C

 q = ne

अतः
q = 100 x 1.6 x 10^-19
q = 1.6 x 10^-17C

(adsbygoogle = window.adsbygoogle || []).push({});

Question.3 –

एक पॉलिथीन के टुकड़े को उनसे रगड़ने पर 3 x 10-7 आवेश आ जाता है। इस प्रक्रिया में कितने आवेश स्थानांतरित हुए? क्या इसमें द्रव्यमान भी स्थानांतरित होगा?
Solution

 q = ne
-3 x 10^-7 = n(-1.6 x 10^-19C)
n = -3 x 10^-7/(-1.6 x 10^-19C)

n = 2

द्रव्यमान में वृद्धि
m = 2 x 10¹² x 9.1 x 10^-31
= 18.2 x 10^-19 Kg

Question.4

किसी पिंड से 1 सेकंड में  10⁹ इलेक्ट्रॉन किसी अन्य पिंड में स्थानांतरित होते हैं तो एक कूलाम के स्थानांतरण में कितना समय लगेगा?

Solution    एक सेकंड में स्थानांतरित इलेक्ट्रॉनों की संख्या = 10⁹
एक कूलाम आवेश में इलेक्ट्रॉनों की संख्या
q= ne
n = q/e = 1/1.6 x 10^-19C
n = 6.25 x 10^-18
t = कुल इलेक्ट्रॉनों की संख्या / एक सेकंड में स्थानांतरित इलेक्ट्रॉनों की संख्या
t = 6.25 x 10¹⁸/ 10⁹
= 6.25 x 10⁹ सेकंड

Question.5

एक सिक्के से कितने इलेक्ट्रॉन निकाले जाए कि उस 10^-7C पर आवेश आ जाए?
Solution        q= ne
10^-7 = n (1.6 x 10^-19)
n = q/e
= 10^-7 / (1.6 x 10^-19)
= 6.25 x 10¹¹ इलेक्ट्रॉन

Question.6

एक कप जल में कितने धन आवेश तथा ऋण आवेश होते हैं?

Solution जल का द्रव्यमान  = 250gm
जल का अणुभार = 18
250 ग्राम जल में अणुओं की संख्या =
n =(m/M) x N_A

= ( 250/18 ) x 6.02 x 10²³

जल के अणु 10 प्रोटोन व 10 इलेक्ट्रॉन होते हैं (2 प्रोटोन तथा इलेक्ट्रॉन हाइड्रोजन के तथा 8 ऑक्सीजन के) तथा धनायन ऋणायन आवेश का मान सम्मान होगा।

एक कप में जल में धनात्मक आवेश
q= ne

q = 10 x (250/18) x 6.02 x 10²³ x 1.6 x 10^-19

q = 12.5 x 10⁶C

आवेश की निश्चरता (Invariance of Electric Charge)

किसी कण पर विद्युत आवेश उसके वेग पर निर्भर नहीं करता है। अतः

विरामावस्था में आवेश = गतिमान अवस्था में आवेश

q_{विरामावस्था} = q_{गतिमान}

विशिष्ट आवेश (Specific Charge)

किसी कण के आवेश q तथा इसके द्रव्यमान m का अनुपात उस कण का विशिष्ट आवेश (Specific Charge) कहलाता है

विशिष्ट आवेश (Specific Charge) = q/m

कुलाम का नियम (Coulomb’s Law)

इस नियम के अनुसार दो स्थिर आवेशों के मध्य लगने वाला आकर्षण या प्रतिकर्षण बल दोनों आवेशों के परिमाण के गुणनफल के समानुपाती तथा दोनों आवेशों के बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।

अतः

f ∝ q₁ q₂ …………1

[katex]f\ \propto{}\frac{1}{r^2}[/katex] ………………2

समीकरण (1) तथा (2) से

[katex]\mathrm{f} \propto \frac{q_{1} q_{2}}{r^{2}} [/katex]

[katex]f=K \frac{q_{1} q_{2}}{r^{2}} [/katex]

K = कुलाम बल नियतांक

[katex]\mathrm{K}=\frac{1}{4 \pi \epsilon_{0}}[/katex]

[katex] f=K \frac{q_{1} q_{2}}{r^{2}} [/katex]

ϵ₀ = निर्वात की विद्युतशीलता

[katex] \epsilon_{0}=8.85 \times 10^{-12} \frac{c^{2}}{N m^{2}}[/katex]

यदि दोनों आवेशों के मध्य माध्यम उपस्थित हो तो

[katex]f_{m}=\frac{1}{4 \pi \epsilon_{0}} \times \frac{q_{1} q_{2}}{r^{2}}[/katex]

f_m = माध्यम की विद्युतशीलता

कुलाम बल नियतांक (K) का मान ज्ञात करना

[katex] K=\frac{1}{4 \pi  \epsilon_{0}} [/katex]

[katex] \mathrm{K}=\frac{1}{4 \times 3.14 \times 8.85 \times 10^{-12}} [/katex]

[katex] \mathrm{K}=\frac{10^{12} \times 10^{4}}{4 \times 314 \times 885} [/katex]

K = 9.009  10⁹

[katex] \mathrm{K}=9.009 \times 10^{9} \sim 9 \times 10^{9} \frac{\mathrm{Nm}^{2}}{\mathrm{c}^{2}} [/katex]

कूलाॅम के नियम का सदिश रुप (Coulomb’s law in vector form)

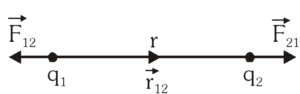
q1 पर q2 के कारण बल

[katex] \overrightarrow{F_{12}}=K \frac{q_{1} q_{2}}{r^{2}} \hat{r}_{21} [/katex]

[katex] \overrightarrow{F_{21}}=K \frac{q_{1} q_{2}}{r^{2}} \hat{r}_{12} [/katex]

यहाँ [katex]  \hat{r}_{12} [/katex] q1 से q2 की ओर एंकाक सदिश है।

[katex] \overrightarrow{\mathrm{F}}_{12}=\frac{\mathrm{kq}_{1} \mathrm{q}_{2}}{\left|\overrightarrow{\mathrm{r}}_{1}-\overrightarrow{\mathrm{r}}_{2}\right|^{3}}\left(\overrightarrow{\mathrm{r}}_{1}-\overrightarrow{\mathrm{r}}_{2}\right) [/katex]

अध्यारोपण का सिद्धांत (Principle of superposition)

इस नियमानुसार जब कई आवेशों के बीच में स्थिरवैद्युतिकी अन्योन्य क्रिया होती है तो आवेश पर लगने वाला कुल स्थिरवैद्युतिकी बल, अन्य आवेशों के द्वारा लगाए गए बलों के सदिश योग के तुल्य होता है।

अतः

[katex]  \mathrm{F}=\frac{\mathrm{kq}_{0} \mathrm{q}_{1}}{\mathrm{r}_{1}^{2}}+\frac{\mathrm{kq}_{0} \mathrm{q}_{2}}{\mathrm{r}_{2}^{2}}+\cdots+\frac{\mathrm{kq}_{0} \mathrm{q}_{\mathrm{i}}}{\mathrm{r}_{\mathrm{i}}^{2}}+\ldots \frac{\mathrm{kq}_{0} \mathrm{q}_{\mathrm{n}}}{\mathrm{r}_{\mathrm{n}}^{2}} [/katex]

इन्हें भी पढ़े –

• प्रकाश का परावर्तन, समतल दर्पण तथा गोलीय दर्पण
• प्रकाश का अपवर्तन तथा लेंस
• स्थिर विद्युतिकी, विद्युत आवेश की परिभाषा, प्रकार, मात्रा तथा गुणधर्म 
• आवेश का मात्रक एवं आवेशन की विधियां
• आपेक्षिक विद्युतशीलता या पैराविद्युतांक

बाहरी कड़ियाँ

1. visit – PCBM
2. Top 10 high earning YouTubers
3. Best 12 Affordable Web Hosting Services
4.  Please subscribe to our YouTube channel – Aliscience